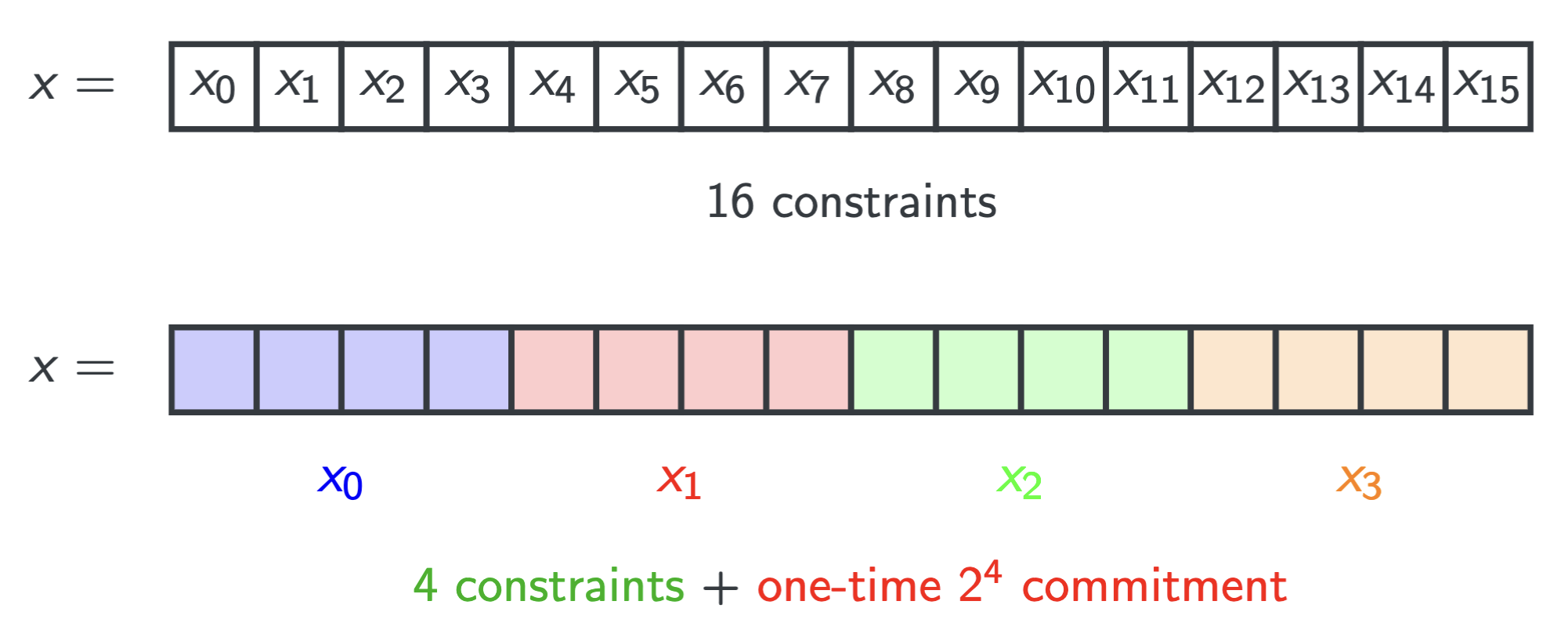
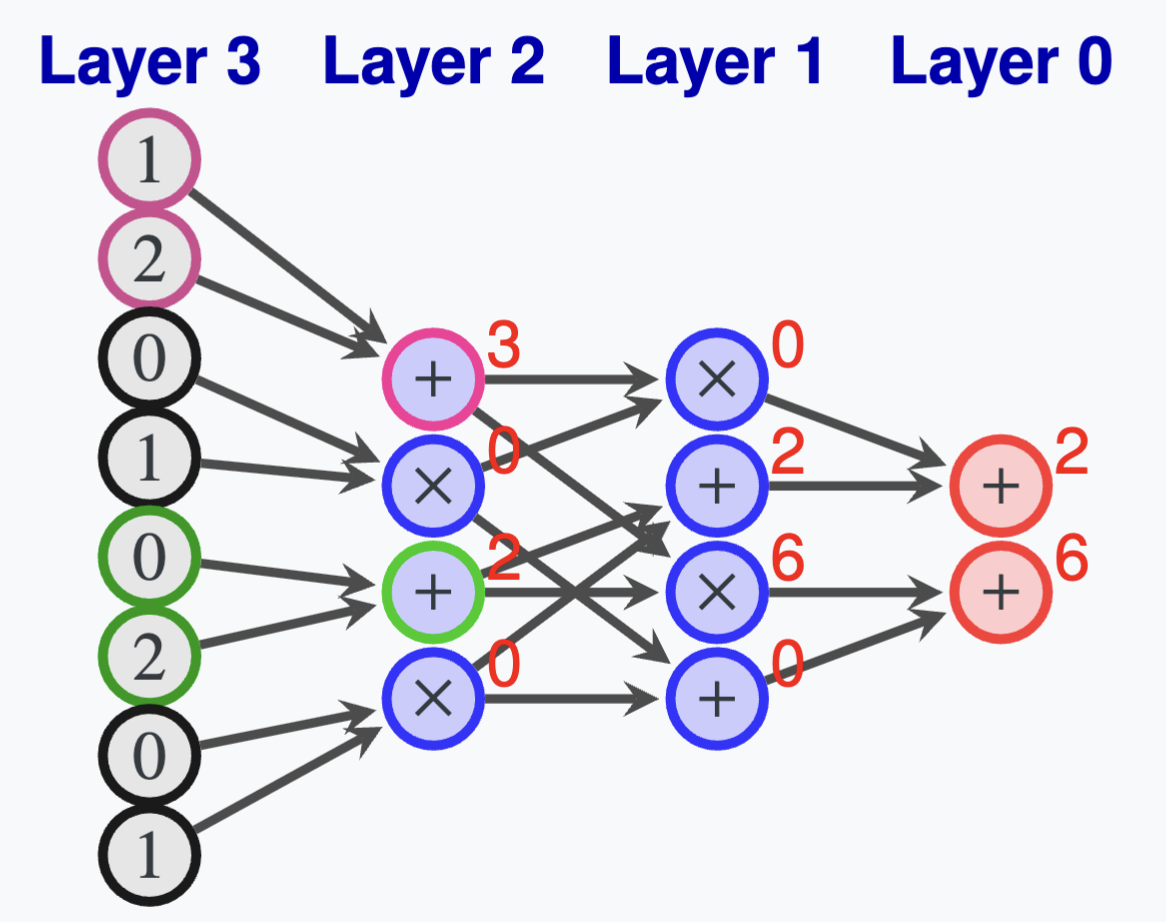
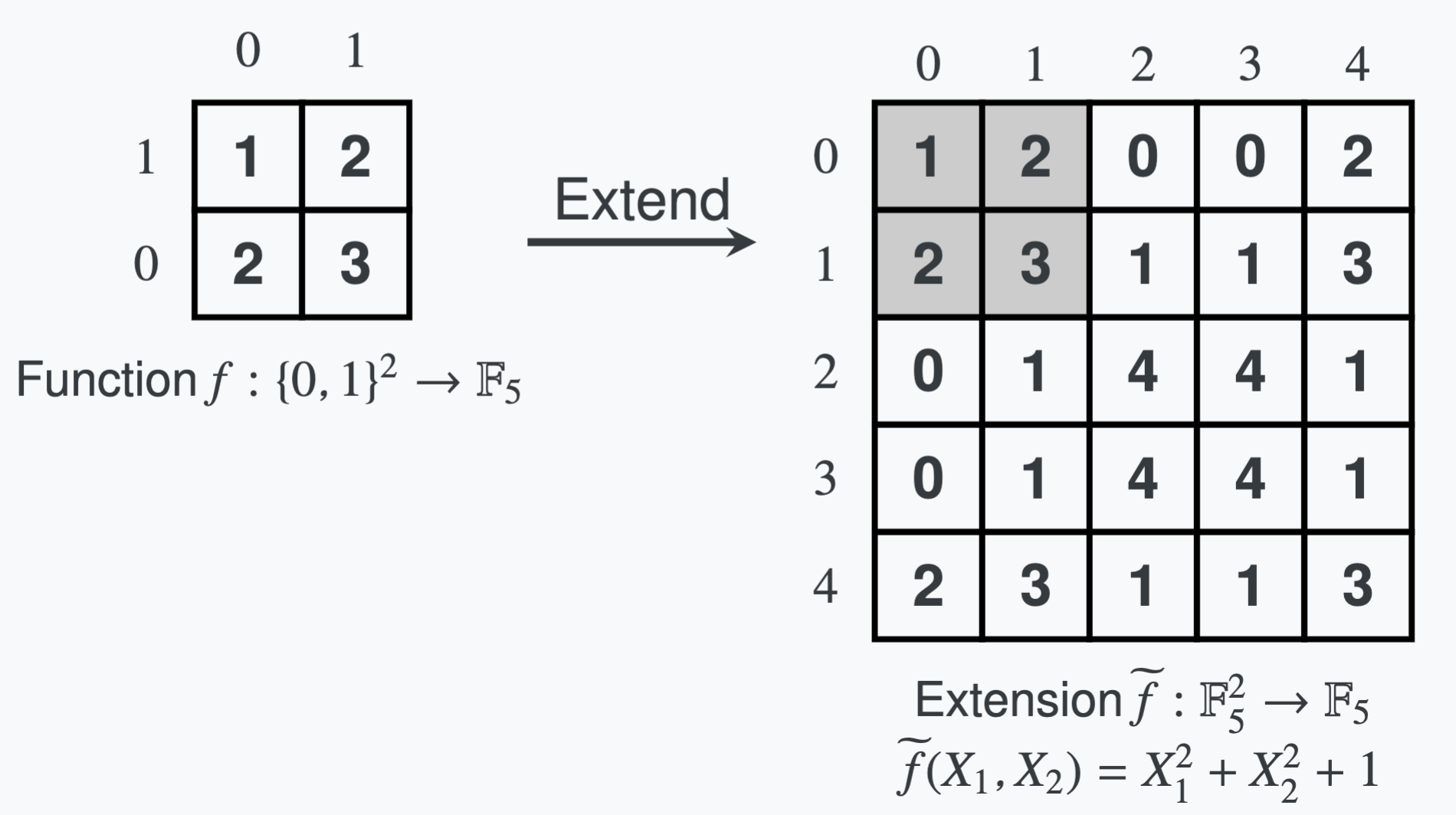
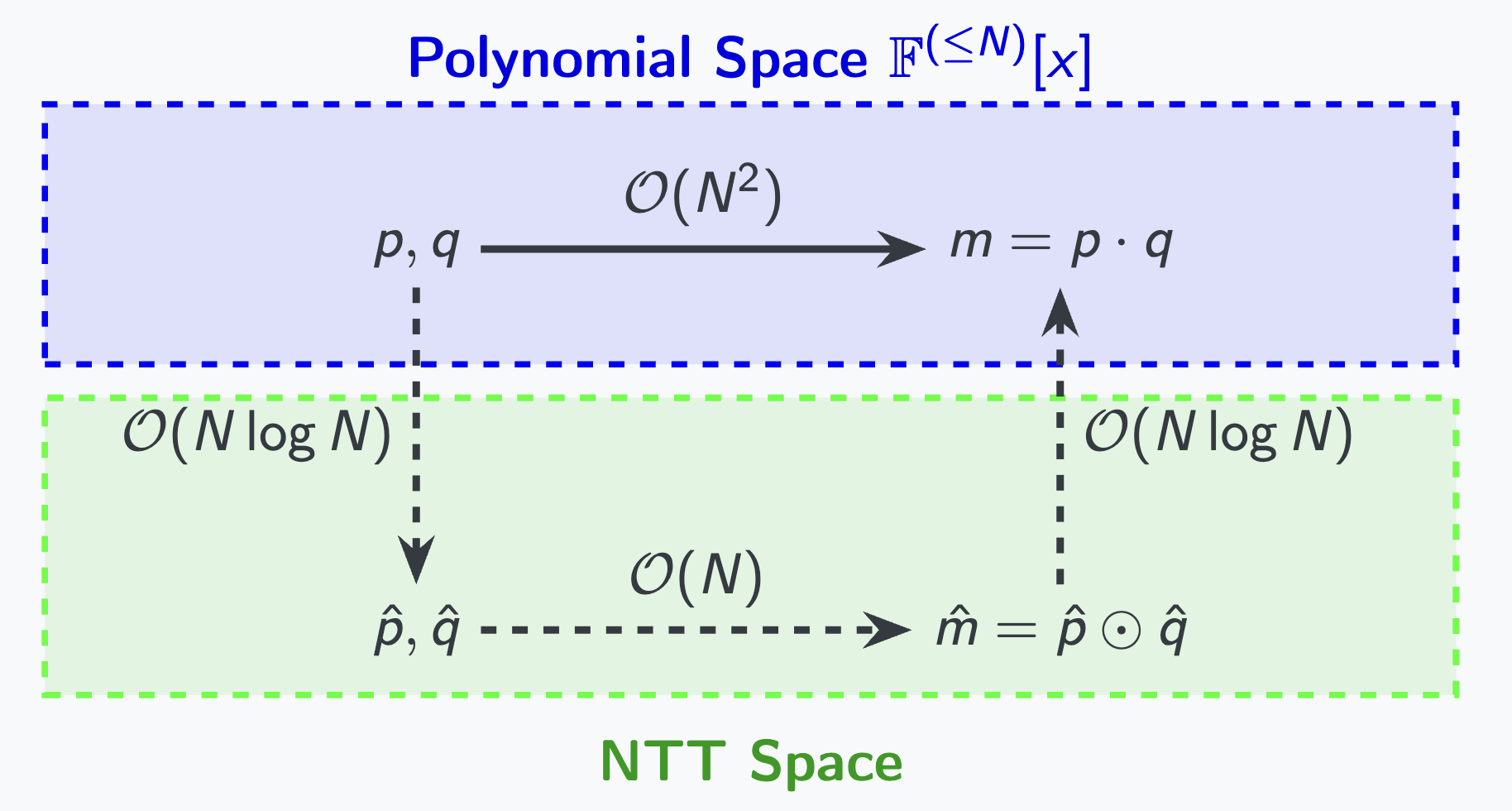
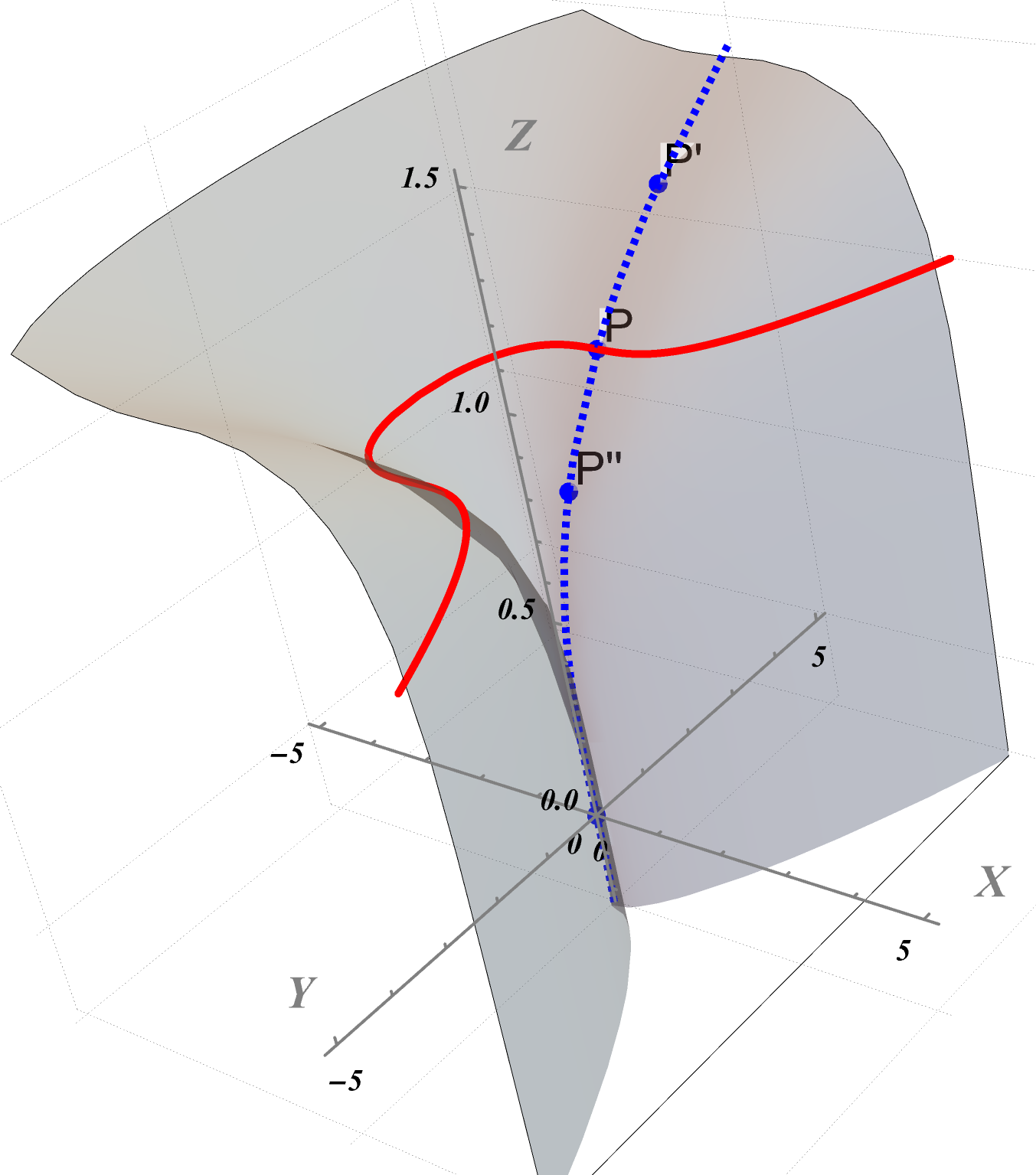
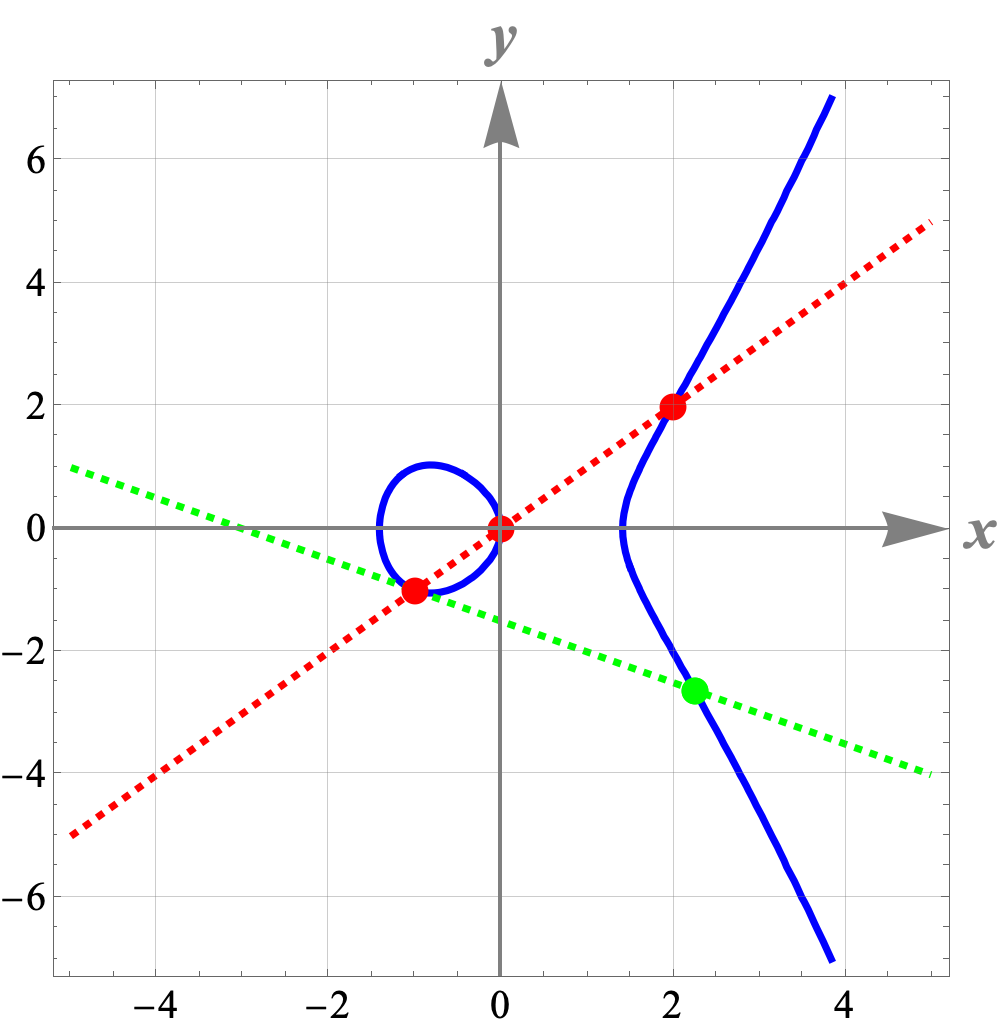
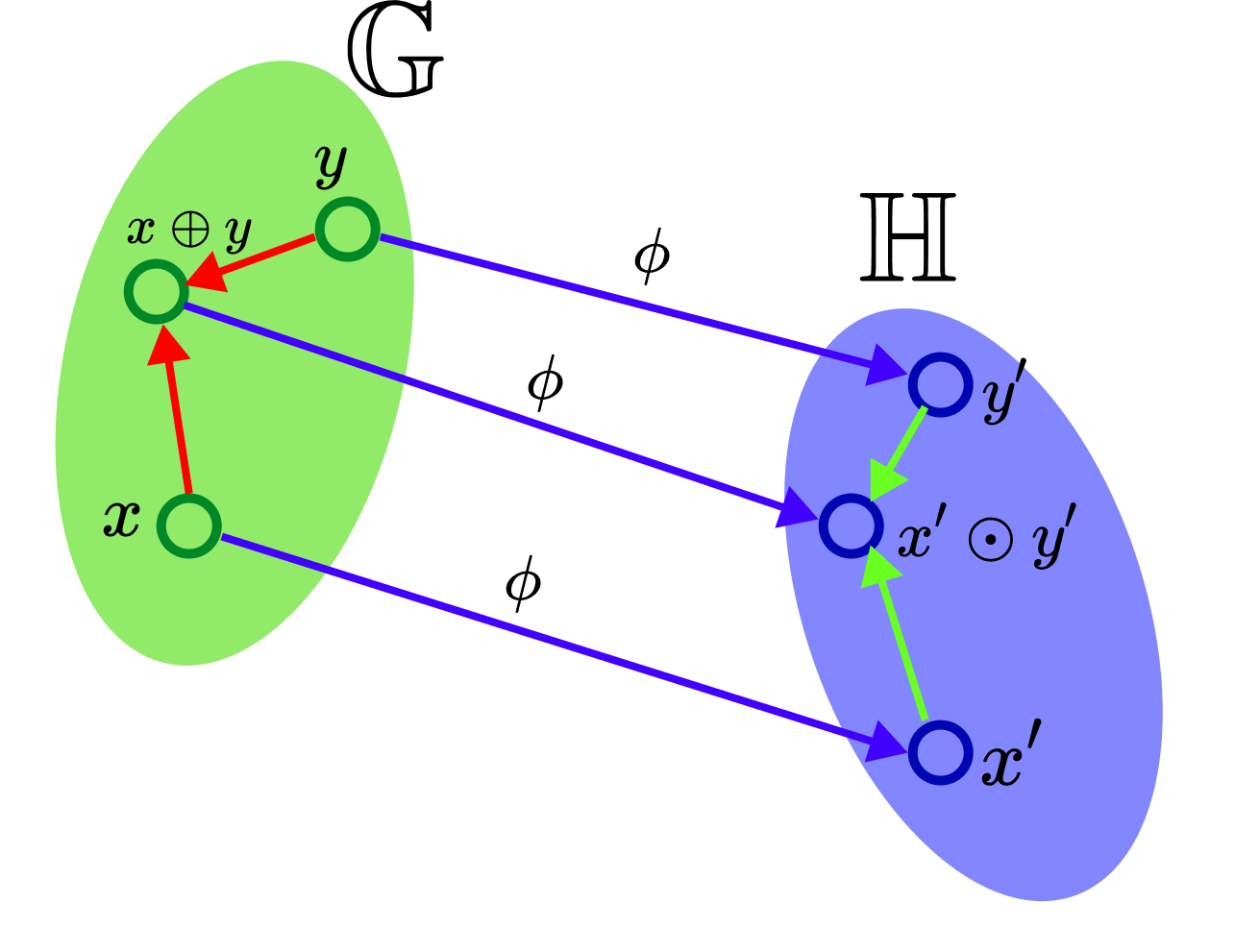
Book
Based on the lecture material, we composed a book, which is available by the link below. Note that the book is still in active development, and we are looking forward to your feedback on it. If you want to contribute, visit our GitHub Repository and leave your comments or pull requests.